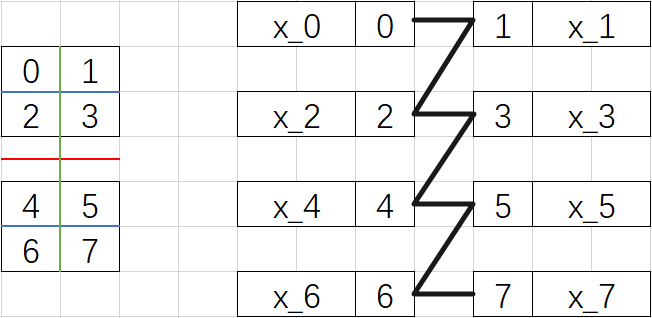1. 背景知识
在开始讲解推导方法前,首先介绍一下Layout的基础知识:
1.1 Layout
Layout是mindspore中用于统一描述Tensor排布的类。
其主要有3个关键成员变量:
- ①device_matrix:设备矩阵,用于描述集群中的卡如何排布。
- ②alias_name:别名,用于指定device_matrix中各个设备维度的名字。
- ③tensor_map:张量映射,用于描述Tensor的各个维度如何切分。
如下代码样例是为一个Tensor配置切分策略的通用模板:
# 设备矩阵,假设一共有8张卡
device_matrix = (2, 4)
# 别名,为了方便起见直接按从左到右的维度顺序命名
alias_name = ("axis_0", "axis_1")
# 张量映射,假设Tensor.shape=(2, 4)
tensor_map = ("axis_0", "axis_1")
layout = Layout(device_matrix, alias_name)
shard_strategy = layout(tensor_map)
下面我们依据这个例子逐一介绍这3个变量的含义.
1.2 device_matrix
设备矩阵,用于描述集群中的卡如何排布,为了便于理解此处以2维设备矩阵为例。
# 设备矩阵
device_matrix = (2, 4)
假设一共有8张卡,根据device_matrix = (2, 4),这8张卡会排布成2*4的矩阵。
1.3 alias_name
别名,用于指定device_matrix中各个设备维度的名字。
# 别名,为了方便起见直接按从左到右的维度顺序命名
alias_name = ("axis_0", "axis_1")
根据alias_name = ("axis_0", "axis_1"),我们可以为设备矩阵中的各个维度标明别名。
1.4 tensor_map
张量映射,用于描述Tensor的各个维度如何切分。
# 张量映射,假设Tensor.shape=(2, 4)
tensor_map = ("axis_0", "axis_1")
其中len(tensor_map) == len(Tensor.shape),对于一个tensor_map,假设tensor_map[i] = j:
- 如果
j = "None",表示张量的第i维度不切分。 - 如果
j = "axis_?",表示沿着设备矩阵的"axis_?"维度切分Tensor的第i维度。
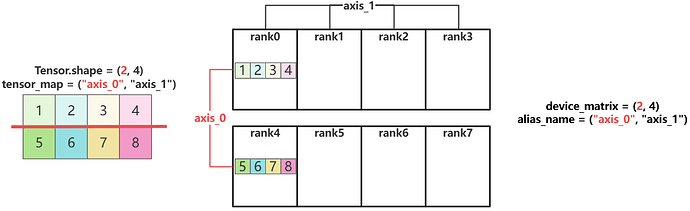
对于样例中的tensor_map = ("axis_0", "axis_1"),构造一个shape = (2, 4)的Tensor,其依据device_matrix和tensor_map的分片过程如下:
- 首先假设将Tensor放在rank0上 ![image]
tensor_map[0] = "axis_0":沿着device_matrix的"axis_0"维度切分Tensor的第0维。
tensor_map[1] = "axis_1":沿着device_matrix的"axis_1"维度切分Tensor的第1维。
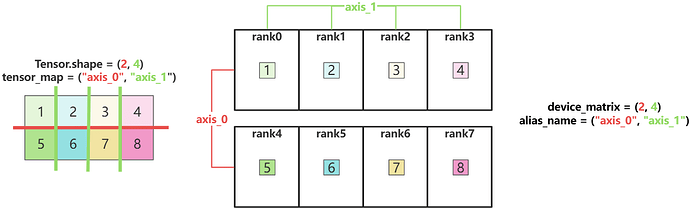
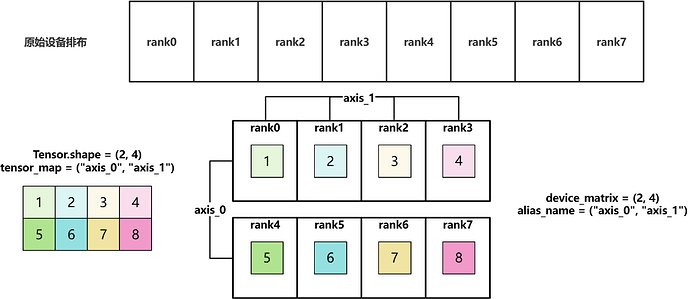
1.5 Tensor分片结果
最终基于如下Layout配置,得到的分片结果如图所示:
# 设备矩阵,假设一共有8张卡
device_matrix = (2, 4)
# 别名,为了方便起见直接按从左到右的维度顺序命名
alias_name = ("axis_0", "axis_1")
# 张量映射,假设Tensor.shape=(2, 4)
tensor_map = ("axis_0", "axis_1")
至此,Layout中的3个关键成员变量介绍完毕。
2. 推导方法
本节先介绍Layout切分下的推导方法,再介绍用shard切分的推导方法。
2.1 Layout切分的推导方法
下面开始介绍推导方法,其实很简单,3步即可完成,一编二调三算:
- ①一编(编号):由右至左对dev_matrix进行各轴n进制编号
- ②二调(调整):依据tensor_map调整dev_matrix编号
- ③三算(分片):依据各轴n进制计算各卡上的Tensor分片号
下面2.1.1/2.1.2和2.1.3分别为8卡(2 * 2 * 2 / 4 * 2)切满和8卡(2 * 2)切不满情况下的推导过程
2.1.1 8卡切满(2 * 2 * 2),无重复
2.1.1.1 一编(编号):由右至左对dev_matrix进行各轴n进制编号
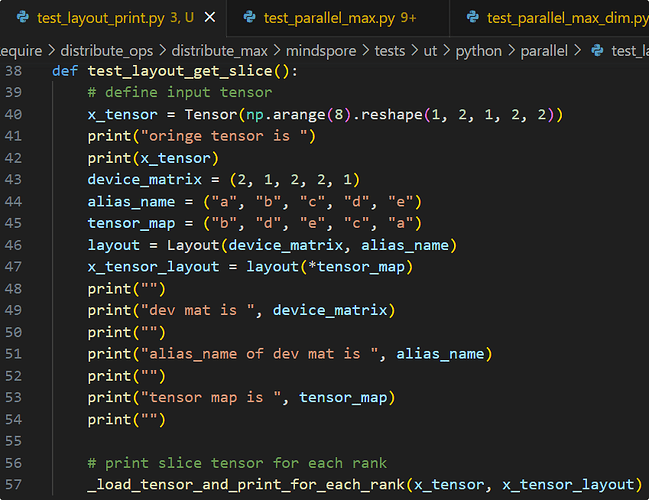
以如下Layout配置为例
layout = Layout((2, 1, 2, 2, 1), ("a", "b", "c", "d", "e"))
in_strategy = (layout("b", "d", "e", "c", "a"),)
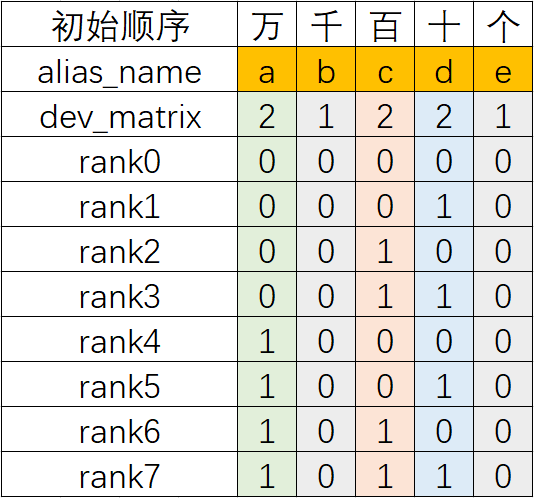
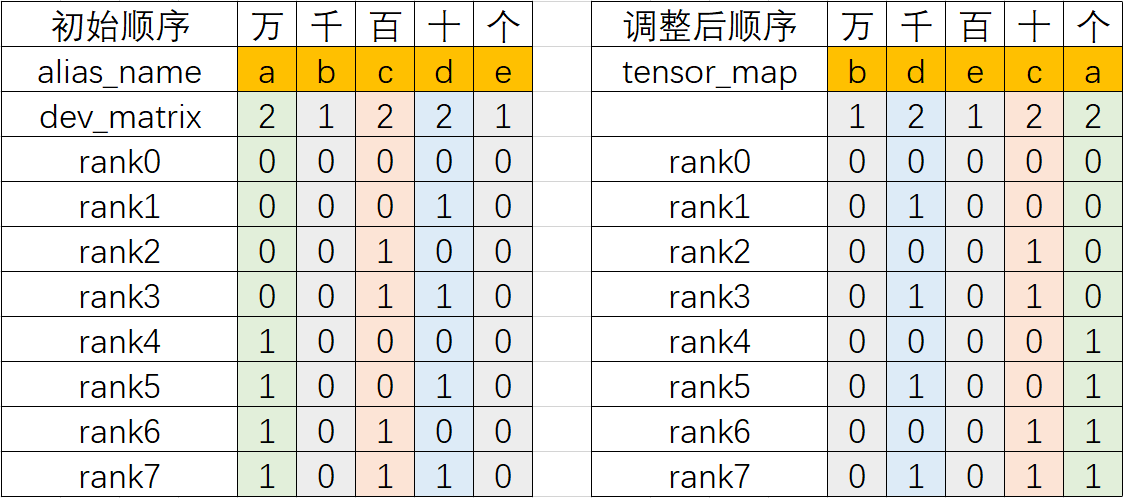
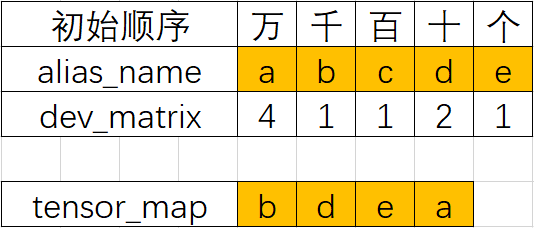
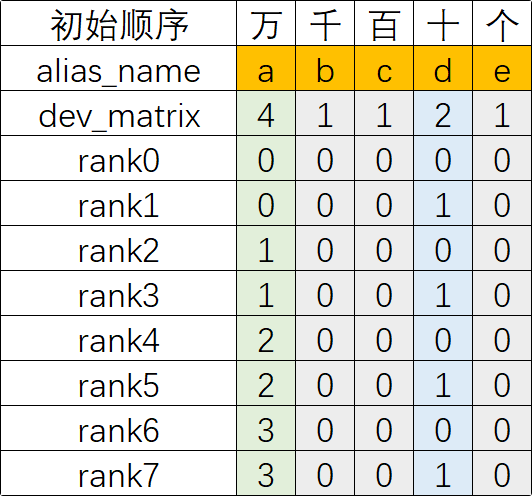
首先从配置可绘制表格:
然后从右至左为dev_matirx进行各轴n进制(从右向左进位)编号,得到如下编号:
- alias_name "e"对应的dev_matrix数值为1(此列为1进制),因此其可以取[0]
- alias_name "d"对应的dev_matrix数值为2(此列为2进制),因此其可以取[0, 1]
- 假设alias_name "x"对应的dev_matrix数值为n(此列为n进制),则其可以取[0, 1, …, n-1]
2.1.1.2 二调(调整):依据tensor_map调整dev_matrix编号
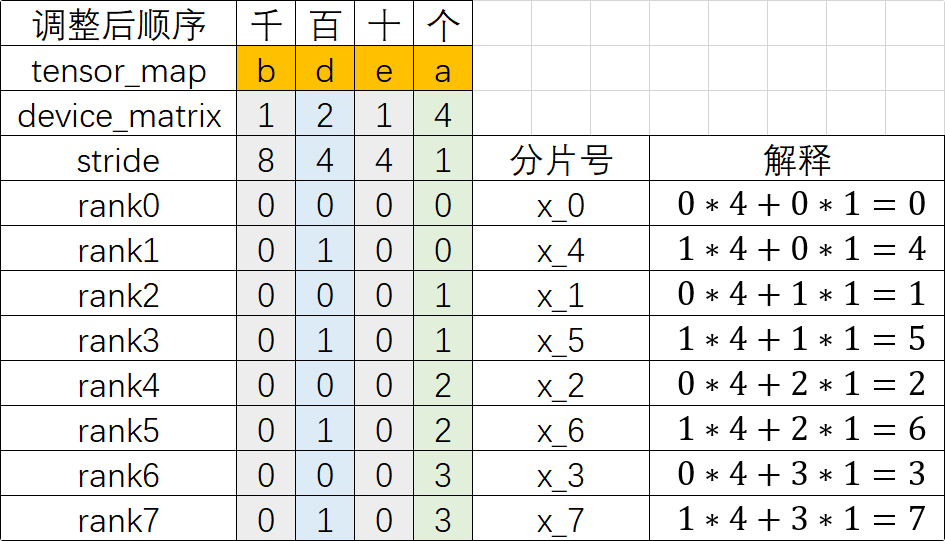
依据tensor_map中的alias_name的顺序调整dev_matrix对应编号列的顺序,得到如下新的dev_matrix编号
2.1.1.3 三算(分片):依据各轴n进制计算各卡上的Tensor分片号
根据新的dev_matrix编号,依据各轴n进制计算各卡上的Tensor分片号。 为了更好理解,这里首先利用各轴的卡数计算出每个device_matrix的步长stride:
- stride[“b”] = device_matrix[“d”] * device_matrix[“e”] * device_matrix[“c”] * device_matirx[“a”] = 2 * 1 * 2 * 2 = 8
- stride[“d”] = device_matrix[“e”] * device_matrix[“c”] * device_matirx[“a”] = 1 * 2 * 2 = 4
- stride[“e”] = device_matrix[“c”] * device_matirx[“a”] = 2 * 2 = 4
- stride[“c”] = device_matirx[“a”] = 2
- stride[“a”] = 1
然后基于stride和每个rank的编号计算出分片号:
- rank_i的分片号 = 各轴的编号 * 各轴的stride,再将所有轴的值累加
依照以上方法即可推导出每张卡对应的Tensor分片号,此处使用分片脚本(后续开放)来验证推导的正确性:
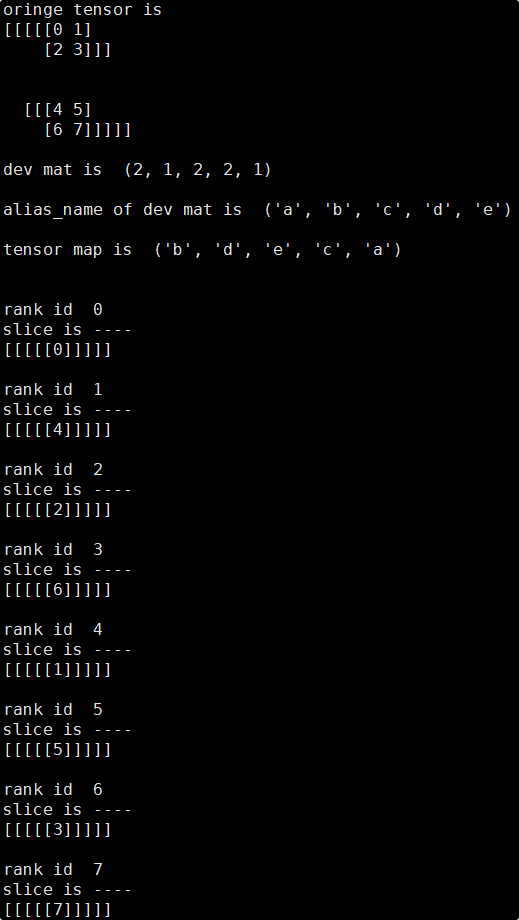
可见输入Tensor如下,其shape为(1,2,1,2,2)
[[[[[0, 1],
[2, 3]]],
[[[4, 5],
[6, 7]]]]]
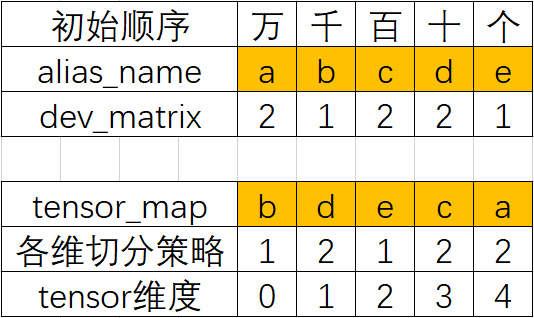
tensor_map对应的各维切分策略如下:
依据tensor_map对Tensor各维度进行切分(分别以红,蓝,绿三个线条表示对第1,3,4 Tensor维度的切分),得到Tensor分片如下,按照Z字型排序:
最后将脚本实际输出结果与上述推导结果进行对比,可见各卡上的tensor分片数值均正确。
2.1.2 8卡切满(4 * 2),无重复
2.1.2.1 一编(编号):由右至左对dev_matrix进行各轴n进制编号
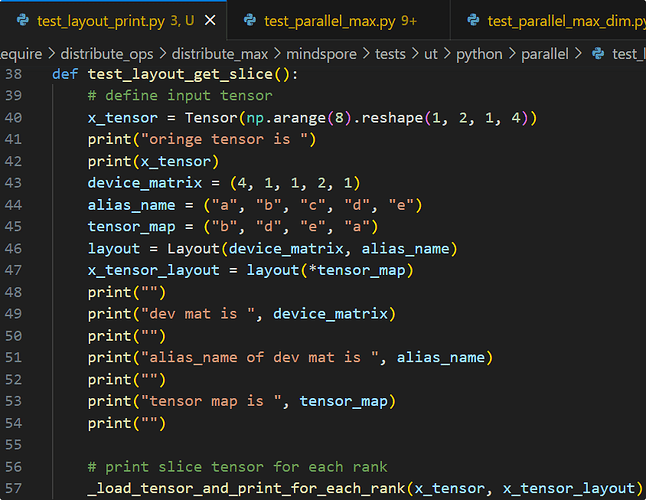
以如下Layout配置为例
layout = Layout((4, 1, 1, 2, 1), ("a", "b", "c", "d", "e"))
in_strategy = (layout("b", "d", "e", "a"),)
首先从配置可绘制表格:
然后从右至左为dev_matirx进行各轴n进制(从右向左进位)编号,得到如下编号:
- alias_name "e"对应的dev_matrix数值为1(此列为1进制),因此其可以取[0]
- alias_name "a"对应的dev_matrix数值为4(此列为4进制),因此其可以取[0, 1, 2, 3],此时"a"列逢4进1
- 假设alias_name "x"对应的dev_matrix数值为n(此列为n进制),则其可以取[0, 1, …, n-1],此时"x"列逢n进1
2.1.2.2 二调(调整):依据tensor_map调整dev_matrix编号
依据tensor_map中的alias_name的顺序调整dev_matrix对应编号列的顺序(注意:tensor_map中没有用到的dev_matrix列直接丢弃即可,比如本例中c列被丢弃),得到如下新的dev_matrix编号
2.1.2.3 三算(分片):依据各轴n进制计算各卡上的Tensor分片号
根据新的dev_matrix编号,依据各轴n进制计算各卡上的Tensor分片号
为了更好理解,这里首先利用各轴的卡数计算出每个device_matrix的步长stride:
- stride[“b”] = device_matrix[“d”] * device_matrix[“e”] * device_matirx[“a”] = 2 * 1 * 4 = 8
- stride[“d”] = device_matrix[“e”] * device_matirx[“a”] = 1 * 4 = 4
- stride[“e”] = device_matirx[“a”] = 4
- stride[“a”] = 1
然后基于stride和每个rank的编号计算出分片号:
- rank_i的分片号 = 各轴的编号 * 各轴的stride,再将所有轴的值累加
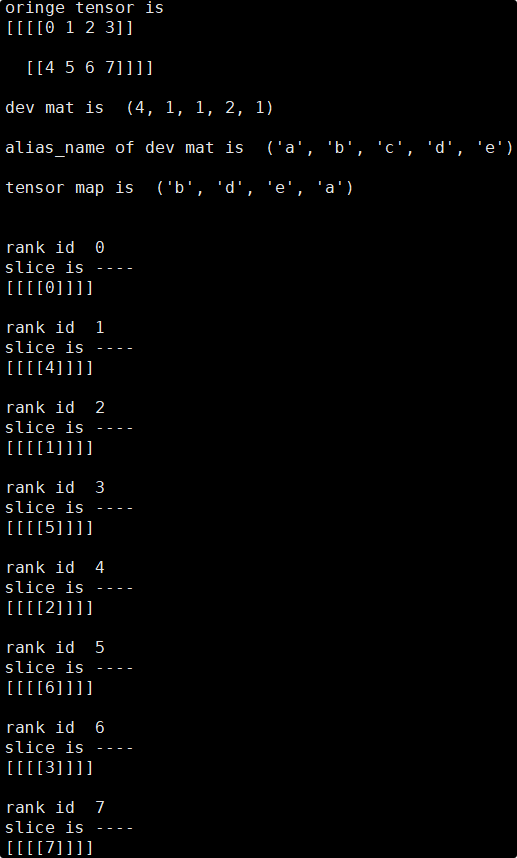
依照以上方法即可推导出每张卡对应的Tensor分片,此处使用分片脚本来验证推导的正确性:
可见实际输出结果与推导结果一致,各卡上的tensor分片数值均正确。
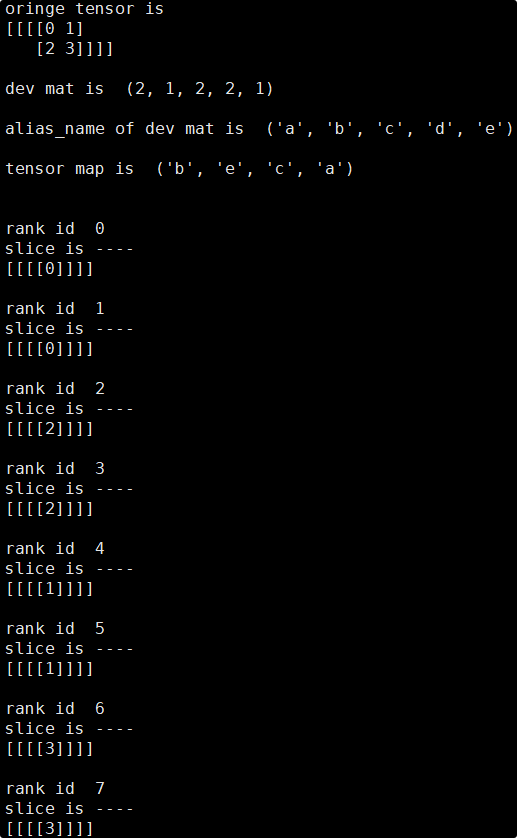
2.1.3 8卡未切满(2 * 2),有重复
2.1.3.1 一编(编号):由右至左对dev_matrix进行各轴n进制编号
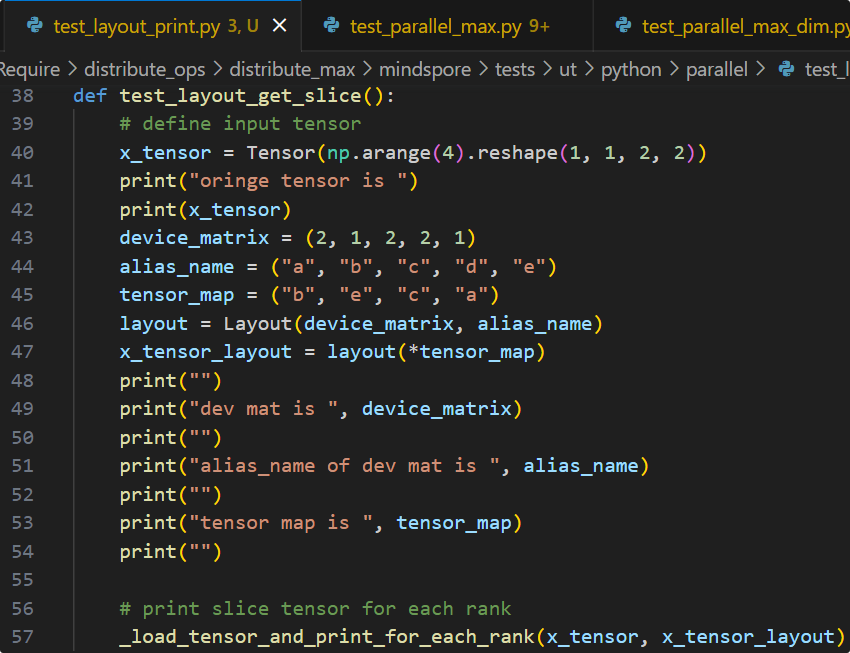
以如下Layout配置为例
layout = Layout((2, 1, 2, 2, 1), ("a", "b", "c", "d", "e"))
in_strategy = (layout("b", "e", "c", "a"),)
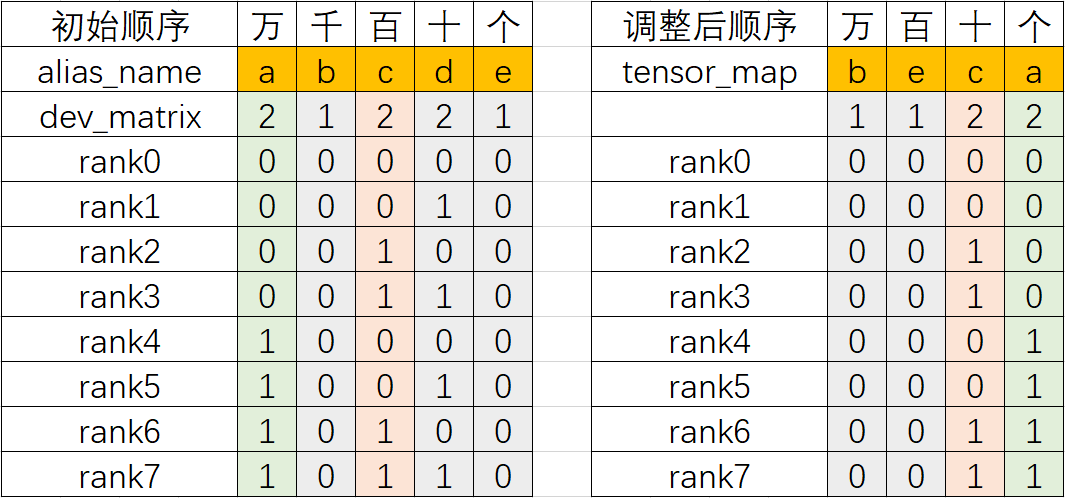
首先从配置可绘制表格:
然后从右至左为dev_matirx进行各轴n进制(从右向左进位)编号,得到如下编号:
2.1.3.2 二调(调整):依据tensor_map调整dev_matrix编号
依据tensor_map中的alias_name的顺序调整dev_matrix对应编号列的顺序(注意:tensor_map中没有用到的dev_matrix列直接丢弃即可,比如本例中d列被丢弃),得到如下新的dev_matrix编号
2.1.3.3 三算(分片):依据各轴n进制计算各卡上的Tensor分片号
根据新的dev_matrix编号,依据各轴n进制计算各卡上的Tensor分片号 为了更好理解,这里首先利用各轴的卡数计算出每个device_matrix的步长stride:
- stride[“b”] = device_matrix[“e”] * device_matrix[“c”] * device_matirx[“a”] = 1 * 2 * 2 = 4
- stride[“e”] = device_matrix[“c”] * device_matirx[“a”] = 2 * 2 = 4
- stride[“c”] = device_matirx[“a”] = 2
- stride[“a”] = 1
然后基于stride和每个rank的编号计算出分片号:
- rank_i的分片号 = 各轴的编号 * 各轴的stride,再将所有轴的值累加
依照以上方法即可推导出每张卡对应的Tensor分片,此处使用分片脚本来验证推导的正确性:
可见实际输出结果与推导结果一致,各卡上的tensor分片数值均正确。
2.2 .shard切分的推导方法
这一节介绍通过.shard()方法配置切分策略的分片推导方法
下面开始介绍推导方法,.shard()方法比Layout切分更简单,2步即可完成,一编二算:
- ①一编(编号):由右至左对dev_matrix进行各轴n进制编号
- ②二算(分片):依据各轴n进制计算各卡上的Tensor分片号
下面2.2.1和2.2.2分别为8卡切满和8卡切不满情况下的推导过程
2.2.1 8卡切满,无重复
2.2.1.1 一编(编号):由右至左对dev_matrix进行各轴n进制编号
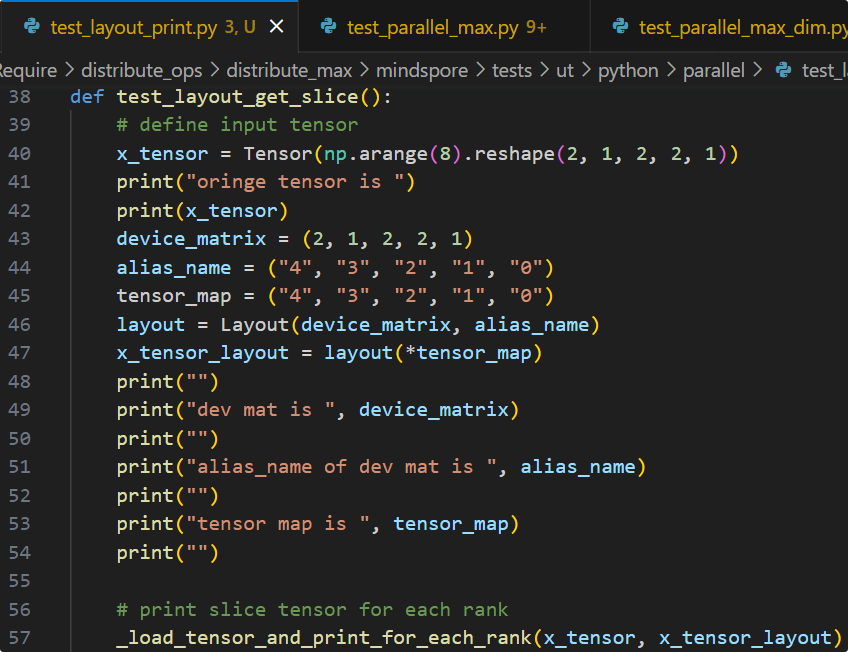
以如下input_strategy配置为例
input_strategy = ((2, 1, 2, 2, 1),)
.shard流程会根据输入的input_strategy自动计算dev_matrix和tensor_map,简单来说一般dev_matrix==input_strategy,而tensor_map为从右往左的编号,因此得到如下dev_matrix和tensor_map:
dev_matrix= ((2, 1, 2, 2, 1),)
tensor_map=(4, 3, 2, 1, 0)
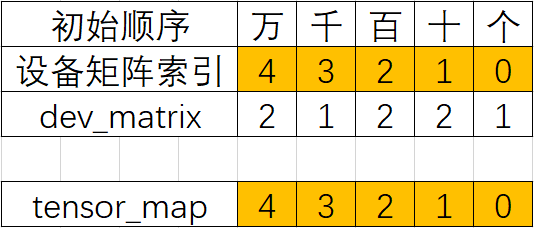
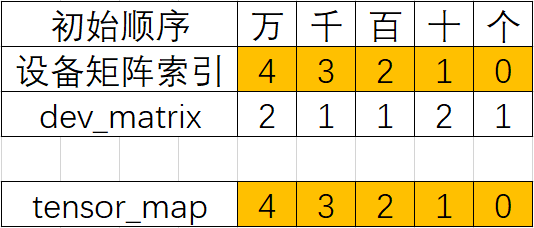
首先从配置可绘制表格:
可以看出此时tensor_map的元素的其实就是dev_matrix从右至左的索引号(索引号其实就可以看做是一个别名,即Layout配置中的alias_name),并且顺序是固定的从右到左,因此压根不需要依据tensor_map来调整dev_matrxi的顺序,这也是为什么比Layout配置少了“二调(调整):依据tensor_map调整dev_matrix编号”这一步的原因。
然后从右至左为dev_matirx进行各轴n进制(从右向左进位)编号,得到如下编号:
- 索引0对应的dev_matrix数值为1(此列为1进制),因此其可以取[0]
- 索引1对应的dev_matrix数值为2(此列为2进制),因此其可以取[0, 1],此时索引1列逢2进1
- 假设索引对应的dev_matrix数值为n(此列为n进制),则其可以取[0, 1, …, n-1]
2.2.1.2 二算(分片):依据各轴n进制计算各卡上的Tensor分片号
根据新的dev_matrix编号,依据各轴n进制计算各卡上的Tensor分片号 为了更好理解,这里首先利用各轴的卡数计算出每个device_matrix的步长stride:
- stride[4] = device_matrix[3] * device_matrix[2] * device_matirx[1] * device_matrix[0]= 1 * 2 * 2 * 1 = 4
- stride[3] = device_matrix[2] * device_matirx[1] * device_matrix[0] = 2 * 2 * 1 = 4
- stride[2] = device_matirx[1] * device_matrix[0] = 2 * 1 = 2
- stride[1] = device_matrix[0] = 1
- stride[0] = 1
然后基于stride和每个rank的编号计算出分片号:
- rank_i的分片号 = 各轴的编号 * 各轴的stride,再将所有轴的值累加
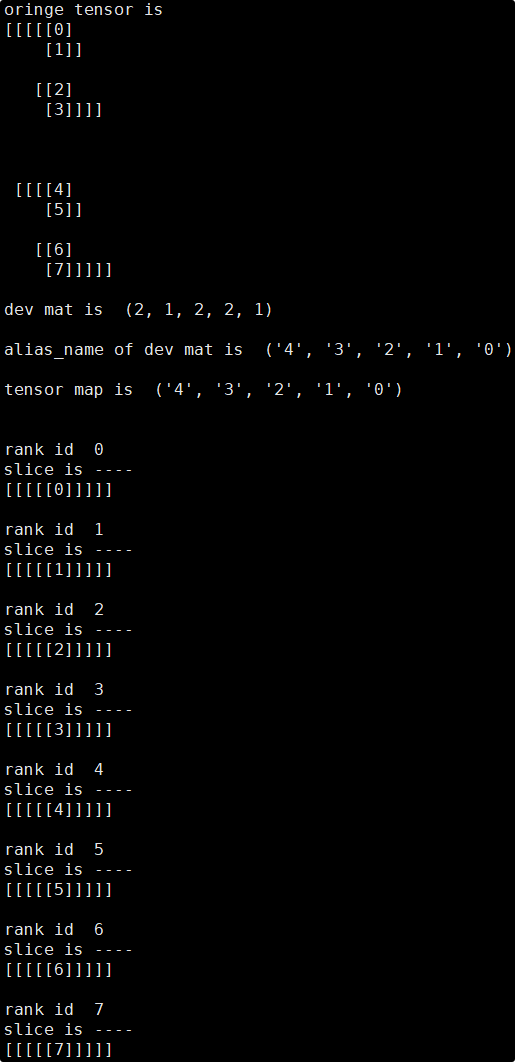
依照以上方法即可推导出每张卡对应的Tensor分片,此处使用分片脚本来验证推导的正确性(此处使用layout来模拟.shard的切分配置):
可见实际输出结果与推导结果一致,各卡上的tensor分片数值均正确。
2.2.2 8卡未切满,有重复
2.2.2.1 一编(编号):由右至左对dev_matrix进行各轴n进制编号以如下input_strategy配置为例
input_strategy = ((2, 1, 1, 2, 1),)
.shard流程会根据输入的input_strategy自动计算dev_matrix和tensor_map,简单来说一般dev_matrix==input_strategy,而tensor_map为从右往左的编号,因此得到如下dev_matrix和tensor_map:
dev_matrix= ((2, 1, 1, 2, 1),)
tensor_map=(4, 3, 2, 1, 0)
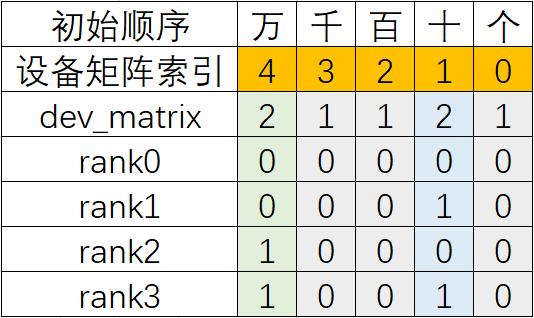
首先从配置可绘制表格:
可以看出此时tensor_map的元素的其实就是dev_matrix从右至左的索引号(索引号其实就可以看做是一个别名,即Layout配置中的alias_name),并且顺序是固定的从右到左,因此压根不需要依据tensor_map来调整dev_matrxi的顺序,这也是为什么比Layout配置少了“二调(调整):依据tensor_map调整dev_matrix编号”这一步的原因。
然后从右至左为dev_matirx进行各轴n进制(从右向左进位)编号,得到如下编号:
- 索引0对应的dev_matrix数值为1(此列为1进制),因此其可以取[0]
- 索引1对应的dev_matrix数值为2(此列为2进制),因此其可以取[0, 1]
- 假设索引对应的dev_matrix数值为n(此列为n进制),则其可以取[0, 1, …, n-1]
2.2.2.2 二算(分片):依据各轴n进制计算各卡上的Tensor分片号
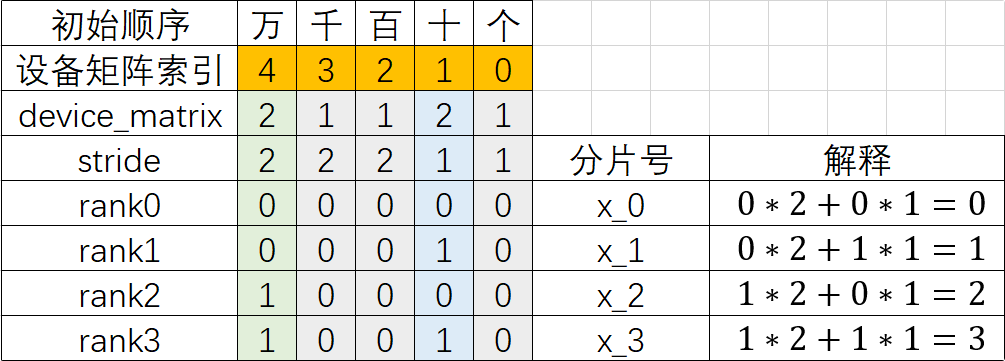
根据新的dev_matrix编号,依据各轴n进制计算各卡上的Tensor分片号 为了更好理解,这里首先利用各轴的卡数计算出每个device_matrix的步长stride:
- stride[4] = device_matrix[3] * device_matrix[2] * device_matirx[1] * device_matrix[0]= 1 * 1 * 2 * 1 = 2
- stride[3] = device_matrix[2] * device_matirx[1] * device_matrix[0] = 1 * 2 * 1 = 2
- stride[2] = device_matirx[1] * device_matrix[0] = 2 * 1 = 2
- stride[1] = device_matrix[0] = 1
- stride[0] = 1
然后基于stride和每个rank的编号计算出分片号:
- rank_i的分片号 = 各轴的编号 * 各轴的stride,再将所有轴的值累加
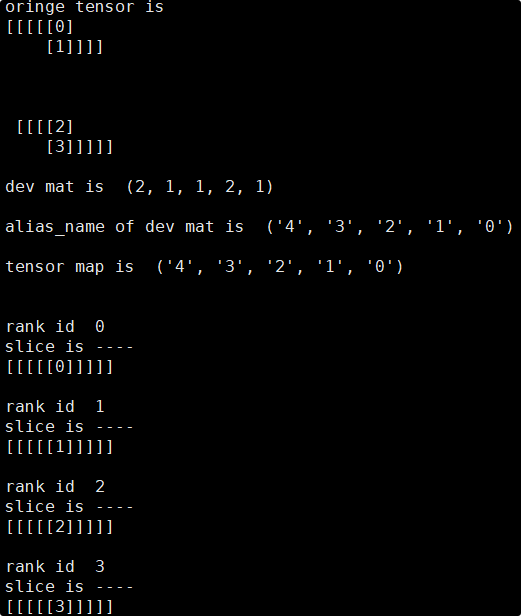
依照以上方法即可推导出每张卡对应的Tensor分片,此处使用分片脚本来验证推导的正确性(此处使用layout来模拟.shard的切分配置):
可见实际输出结果与推导结果一致,各卡上的tensor分片数值均正确。